A星寻路算法

参考资料

Amit’s A* Pages

---

A星算法只是一个寻路算法，需要有配套数据结构支撑。寻路数据结构见：[[寻路导航网格]]

A星算法

1. A星算法只选择当前步骤的最优路径，只关注当前的最优解，所以会忽视全局的最优解，走“弯路“是常有的事情。
2. A星是对 [[Dijkstra最短路径算法]] 的一种优化。
3. A星算法是一种启发式算法，由人工预先设定的估算距离作为启发信息辅助计算，搜索会变得更加高效。
4. 平均时间复杂度为 $O(nlogn)$. 最差的情况需要从起点出发将所有格子走一遍，最后才找到目的地。
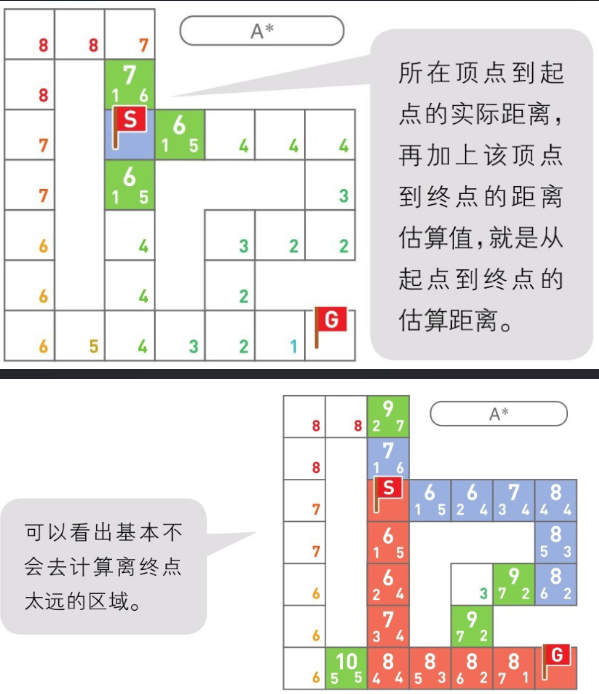
5. 权重：对每个待选的点计算权重，并按照权重排序，权重最小的点被选中。

讲解

A星算法的步骤

1. 先将起点周围的点加入候补队列（优先队列）中，在候补队列中找到与目的地权重最小的点，再把这个点推出来，并以这个点为基准继续向前探索，直到寻找到目的地为止。
2. 权重 = 从起点S到该顶点的距离（方块左下）+ 该顶点距离G的估算值（方块右下）。
3. 

伪代码

function find_path(s,e)
{
    open = new List();  // 没有被取到过的点
    close = new List(); // 已经被取过的点
    
    open.add(s);        // 从s点开始
    close.add(s);       // 将s加入close队列

    for(!open.IsEmpty())// 重复遍历直到没有点可以取
    {
        p = open.pop(); // 把最近的点推出来

        if(p == e)
        {
            // 找到终点
            break;
        }

        p1 = p.left();  // 取左边的点
        p2 = p.right(); // 取右边的点
        p3 = p.top();   // 取上面的点
        p4 = p.down();  // 取下面的点

        plist.add(p1);
        plist.add(p2);
        plist.add(p3);
        plist.add(p4);

        for(int i = 0 ; i<plist.Count ; ++i)
        {
            pp = plist[i];
            if(null != pp && pp.IsNotInClose())
            {
                pp.f = dis(pp,e);
                if(pp.IsNotInOpen())
                {
                    pp.SetOpen();       // 设置为已经在open中
                    open.Add(pp);       // 加入队列
                }
            }
        }

        // p点已经被取过了
        close.add(p);
        // open队列会不断的加入可以行走的点，排序会越来越慢
        open.sort();                  // 进行排序
    }
}

优化方案

1. 场景很大或者很多角色使用A星算法时，会消耗很多CPU时间，从而导致设备性能急剧下降。我们需要对A星做一些优化，从而保持好的性能。
2. open队列会不断的加入可以行走的点，当两点距离很长时，open队列会被塞入很多节点，会使排序速度越来越慢，这个步骤是不可避免的，问题的关键就在于：如何减少open队列中的元素个数，如何加快open队列的排序速度，如何减少搜索次数。
3. A星大部分时间都消耗在了open队列的排序上，所以对open队列的排序做优化是很重要的。

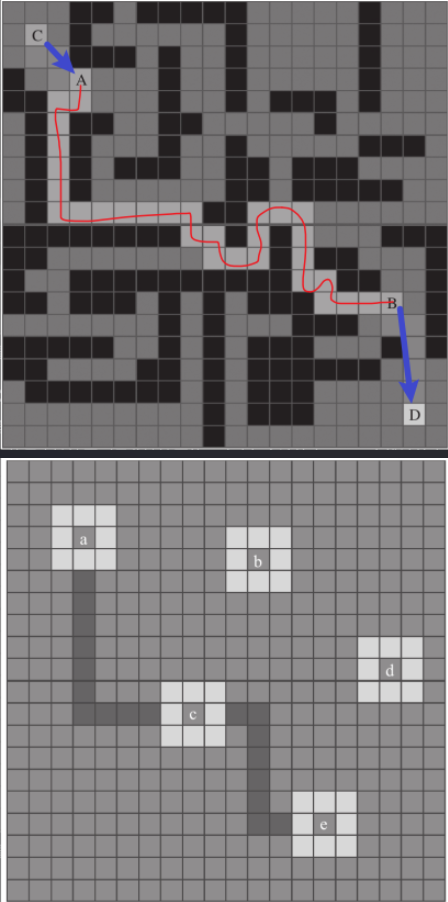
离线缓存路径

1. 路径不一样要实时计算，可以把一些常用的路径离线缓存下来。角色需要寻路时，查询距离起点和目的地最近的缓存路径（A->B），再计算当前位置到路径起点的实时路径（C->A），路径终点的位置到目的地的路径（B->D）,这样把 C->A,A->B,B->D拼起来，就组成了一个完整的从起点到目的地的路径。
2. AB两点通常称为导航点，只要角色附近能够找到导航点，就能直接取出路径直达目的地，节省了大量实时计算路径的时间。
3. 可以在路径上设置一些距离不是太长的导航点，先做导航点寻路，把导航点间的路径连起来作为完整路径链使用。

优化Open队列排序方法

1. 使用[[小根堆]]优先队列数据结构存储open队列，不需要在每次循环结束时重新排序，而是在节点插入最小堆时对最小堆数据结构进行调整。
2. 因为open队列在插入元素前一定是有序的，可以用二分查找算法代替最小堆排序。先使用二分查找算法找到插入的位置，再将元素插入队列，这样每次插入的时间复杂度是 $O(logn+n)$, 这样比快速排序一次的时间复杂度$O(nlogn)$要好一些。

通过权重引导寻路方向

1. 在网格中加入权重值来改变权重从而引导算法寻路走向。权重值小的格子可以组成快速通道
2. 可以令权重 = 当前最近步数 + 当前点到终点的直线步数 + 格子的权重值。

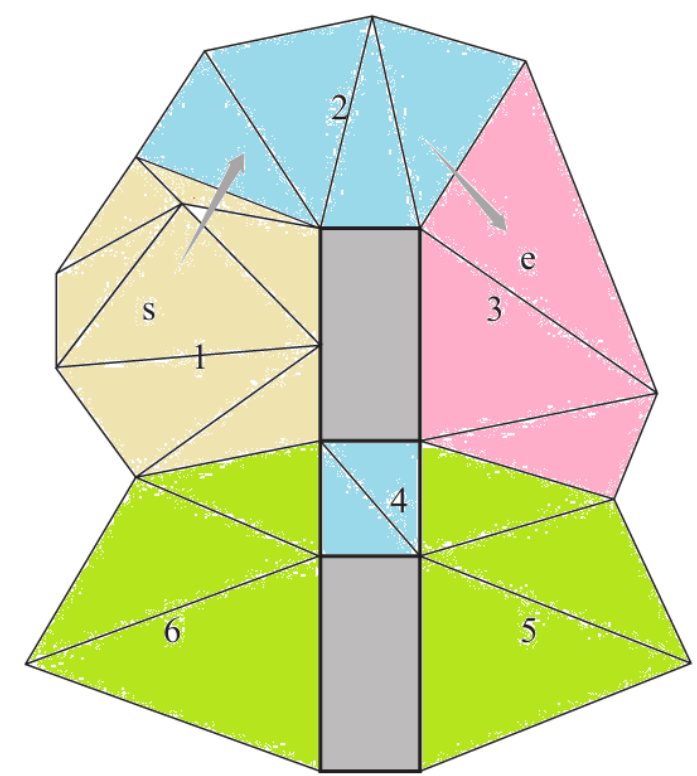
拆分寻路区域

1. 把某个范围内的节点合并为一个区域，把整个地图分成N个大区域，相比于成千上万个格子作为寻路节点要好得多。有了大区域后，只需要寻找大区域间的路径就知道该怎么走，大大降低了搜索的算力。
2. 必须保证拆分之后的可行走区域是凸型，这样区域内就不需要再寻路，任意两个点都是可达的。 - 栅格地图：只能是矩形区域。 - 三角形网格：以凸多边形为单位拆分。
3. 寻路时以区域块为寻路网格，每个区域都记录与之连接的区域以连接点，当算法找到起点与目的地点的区域路径时，只要拼接邻接的路径点就能得出两点的真实路径。
4. 下图为三角形网格用凸多边形划分的区域，s -> 2 -> 3 -> e

减少判断某节点是否被取用过的消耗

1. 当我们查看一个节点是否被取过时，需要判断该节点是否close，有以下几种方法：
   • 在close队列中查找 - 这种做法相当于遍历一次整个close队列，随着close队列里节点的增多，浪费的CPU也越来越多，并且是每次循环都会浪费一次，性能损失巨大。
   • 把节点当成一个实例，添加IsClose变量判断是否被取过 - 这种方法每次寻路前都需要把所有节点都初始化一次，这样做就把A星算法节省下来的性能完全抵消掉了，因此最好不要初始化。
   • 递增一个整形变量值标识是否被取用过 - 寻路类中设置一个全局属性 FindIndex 记录当前的寻路次数，每次寻路前都加一；节点类中也保存一个变量 FindIndex；判断节点时，如果全局和节点的 FindIndex 不同，说明此节点在本次寻路中没有被取用过；当节点被取出时，把节点的 FindIndex 设置成寻路类的 FindIndex，表明此节点被踩过了。(这是一个通用的技巧，任何需要遍历初始化为布尔量的逻辑都可以用此方法避免初始化开销)

     bool function IsClose(Point p)
     {
      returen p.FindIndex == AStar.FindIndex;
     }