Home 渲染管线
Post
Cancel

渲染管线

By Yzngo
Posted 2021-08-20 16 min read

渲染管线

  1. 渲染管线就是GPU完成一次绘制（Drawcall）的过程，经过此流水线的计算，最终将要渲染的画面输出到帧缓存上，最后在屏幕或RT上显示出来。
  2. 渲染管线关注的是每一个drawcall，或者说每一个网格是怎样通过流水线绘制出来的，最后混合时只需要和各种缓冲区（各种全屏缓冲区记录了各种渲染所需要的信息）进行比较，不需要关注其他网格或其他drawcall。

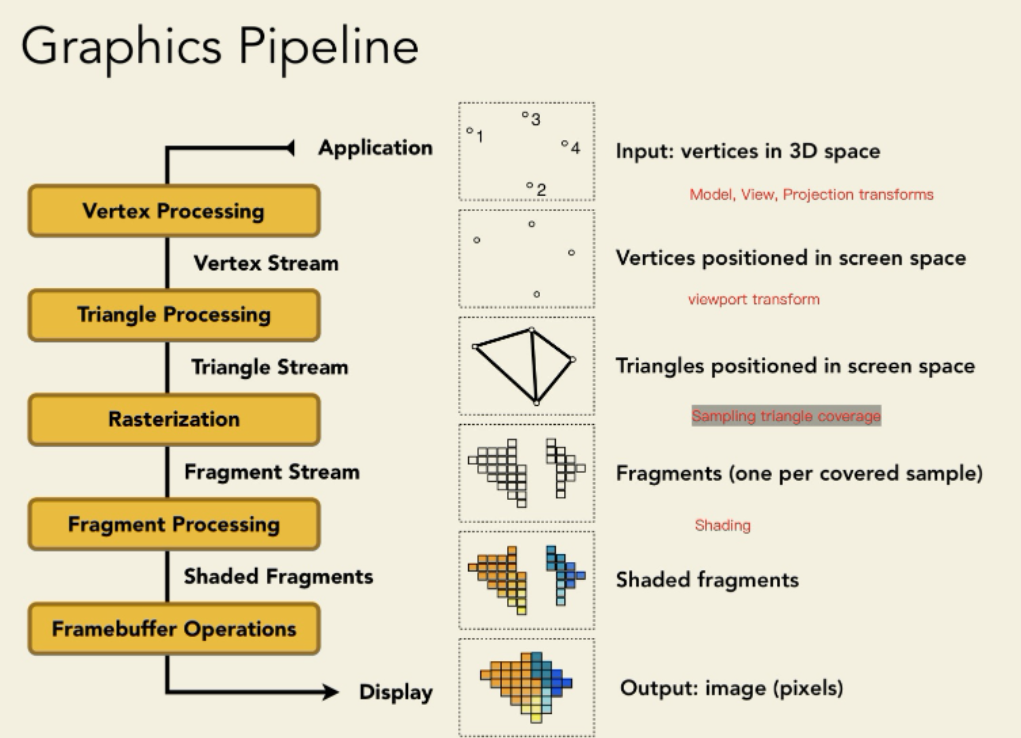
image-20230205185301036

  1. 顶点着色器用于决定三角形应该放在屏幕什么位置。
  2. 片元着色器用于决定三角形范围内的片元拥有什么颜色。
  3. 混合决定最终屏幕像素的颜色值。

应用阶段 - Application Stage

1. 准备渲染需要的数据

  1. 包括决定渲染哪些模型，存在哪些光源，以及摄像头的位置等。
  2. 准备阶段还会做很多优化工作，从而节省渲染时间，提高性能。比如各种粗粒度的 [[Culling]] 剔除。
  3. 把渲染数据(网格或纹理等)加载到[[显存]]中；如果贴图已经存在显存中，不需要重复复制。把数据加载到显存中后，如果CPU不需要这些数据，就可以删除掉。

2. 设置渲染状态

  1. 渲染状态就是一连串的开关或方法。如：是否开启混合，使用哪张纹理，使用哪个 [[Shader]]，是否背面剔除，使用哪些光源等等。
  2. 通俗的讲：设置渲染状态，就是设置并决定接下来的网格如何渲染。
  3. CPU发送了渲染状态改变的指令后，需要控制总线将数据从CPU内存搬运到GPU内存，这个过程会耗费大量时间。
  4. 如果前后渲染的网格渲染状态完全相同，就不需要更改渲染状态。

3. 调用 DrawCall

  1. DrawCall 就是CPU调用 [[图形API]] 向GPU发起的一条渲染指令。
  2. 这个指令指向本次调用需要渲染的图元（点，线，面）列表，不再包含其他渲染信息（之前的渲染状态设置步骤已经设置好了）
  3. 每个模型的每个材质球都会产生一次DrawCall，可以通过各种合批进行优化。
  4. 整个渲染命令队列中，渲染状态切换指令和 Drawcall 指令是交替出现的。

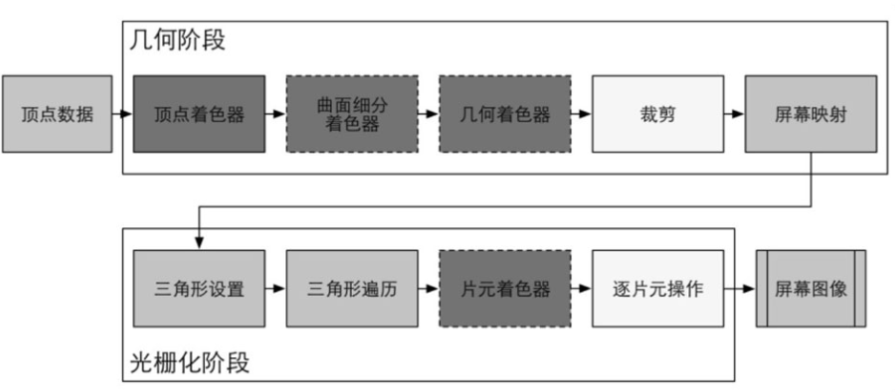
image-20230205185334458

  1. 黑色表示完全可编程
    1. 实线表示必须由开发者实现的着色器
    2. 虚线表示可选的着色器
  2. 白色表示可配置
  3. 灰色表示由GPU固定实现，开发者无控制权

几何阶段 - Geometry Stage

  1. 几何阶段内部也是个小型流水线。
  2. 几何阶段进行逐图元（点，线，三角形）的操作。

1. 顶点着色器 Vertex Shader

  1. 顶点着色器通常用于实现顶点的空间变换，进行顶点着色等。
  2. 输入进来的每一个顶点都会调用一次顶点着色器。
  3. 顶点着色器本身不可以创建或者销毁任何顶点，而且无法得到顶点与顶点之间的关系。
  4. [[顶点动画]] 就是在顶点着色器中改变顶点的位置，可以模拟水面，布料等。
  5. [[3D烘焙动画]] 在顶点着色器中读取新的顶点位置。顶点着色器可以采样贴图）
  6. NDC 坐标：gl_position是归一化的裁剪(NDC)空间坐标，xyz各个维度的范围为-1到1，不带Viewport变换，只能在vertex shader中使用
  7. 顶点着色器把顶点坐标从模型空间变换到齐次裁剪空间。

2. 曲面细分着色器 Tessellation Shader

  1. 可选着色器，用于细分图元。

3. 几何着色器 Geometry Shader

  1. 可选着色器，可以用于产生更多的图元。

4. 裁剪 Clipping

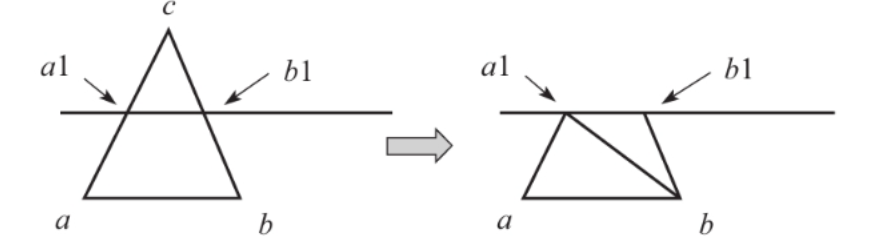
image-20230205185402478

  1. 几何阶段的最后，由NDC坐标判断顶点是落在视口内，还是视口外。
  2. 完全在可视长方体内，数据传递给光栅化阶段。
  3. 完全在可视长方体外，剔除掉。
  4. 一部分在视野内，Clip裁剪掉视口外的部分，生成新的顶点连接边界处。

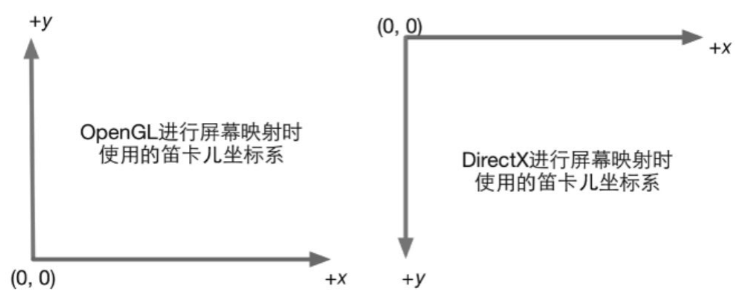
5. 屏幕映射 Screen Mapping

  1. 此阶段负责把每个图元的NDC坐标转换到屏幕坐标。
  2. 屏幕映射得到的屏幕坐标决定了这个顶点对应屏幕上哪个像素（x,y）以及距离这个像素有多远（z）。
  3. 屏幕映射之后输出到光栅化阶段的信息有：顶点的屏幕坐标(x,y)，顶点的深度值(z)，顶点的法线方向等等。

image-20230205185421794

光栅化阶段 - Rasterizer Stage

  1. 光栅化阶段内部也是个小型流水线。
  2. 光栅化阶段有两个主要目标：计算每个图元(三角形)覆盖了哪些像素，以及为这些像素计算颜色。
  3. 光栅化就是屏幕空间的采样。 Rasterization = Sample 2D Positions
  4. 光栅化将屏幕坐标 (0,0) - (w,h) 离散化为一个一个的片元 Fragment (gl_FragCoord)

三角形设置 - Triangle Setup

三角形设置

  1. 三角形设置阶段从屏幕映射得到的信息有：顶点的屏幕坐标(x,y)，顶点的深度值(z)，顶点的法线方向等等。
  2. 三角形设置就是：通过上一阶段得到的三角形网格顶点的屏幕坐标，形成三角形的边，得到三角形边界的表示方式，计算每条边的像素坐标。即把三角形面片铺在屏幕空间坐标平面上。

三角形设置(画线)算法

  1. midpoint 中点算法
  2. Bresenham 直线算法

三角形遍历 - Triangle Traversal

三角形遍历

  1. 三角形遍历也叫扫描变换（Scan Conversion）。
  2. 通过上一阶段得到的三角边，检查每一个三角网格分别覆盖了哪些像素，如果像素被覆盖，就生成一个片元（fragment）。

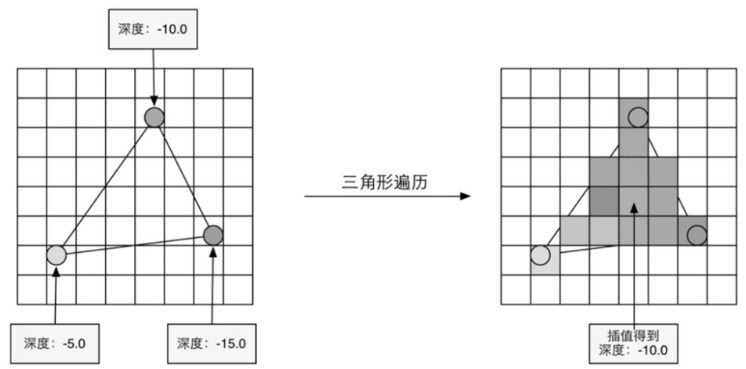
像素插值

  1. 三角形遍历阶段使用三角形重心坐标对3个顶点进行插值，得到片元的信息。插值数据包括：屏幕坐标，像素深度，像素颜色，像素法线，像素UV坐标等。

  2. image-20230205185435997

可选的 Early-Z

Early-Z

  1. Early-Z是指在片元着色器之前做深度测试，丢弃掉测试不通过的片元。
  2. 如果不做Early-Z把被遮挡的片元剔除，则这些片元都要经过片元着色器的计算，可能很浪费性能。

Early-Z 流程

  1. Early-Z 通过GPU硬件自动实现。在正常的渲染之前通过一个超简单的pass（z-pre-pass）进行深度测试。
  2. 如果在片元着色器中主动抛弃片元（比如通过[[半透明物体的Alpha Test]]），Early-Z前置深度测试就会出现问题，因为Early-Z会把主动抛弃的片元后面的片元抛弃掉，画面中可能会留下黑洞，这样画面就不对了。
  3. 如果GPU检测到Fragment Shader中抛弃了片元或者修改了深度值，就会弃用Early-Z。

片元着色器 Fragment Shader

  1. DirectX中叫做 Pixel Shader 像素着色器。

片元着色器

  1. 逐片元执行 Fragment Shader 程序，片元彼此之间不相识。
  2. 片元着色器的输入是三角形遍历时根据从顶点着色器中输出的数据插值得到的。
  3. 片元着色器的输出是一个或多个颜色值。
  4. 片元着色器的功能主要有：纹理采样，改变颜色，计算光照，复杂着色，深度计算，丢弃片元等；最终输出一个像素颜色值。

逐片元操作 - Per-Fragment Operations

  1. 在DirectX中，这一阶段被称为 输出合并阶段 Output Merger
  2. 此阶段的步骤大都可决定片元的去留问题，如果片元在这几个节点中的任意一个节点没有通过测试，管线就会停止并 discard 它，之后的测试就不会再继续执行；反之，测试全部通过，就会进入混合阶段混合，然后进入帧缓存等待输出到屏幕。

多重采样的片元操作

剪切测试 - Scissor Test

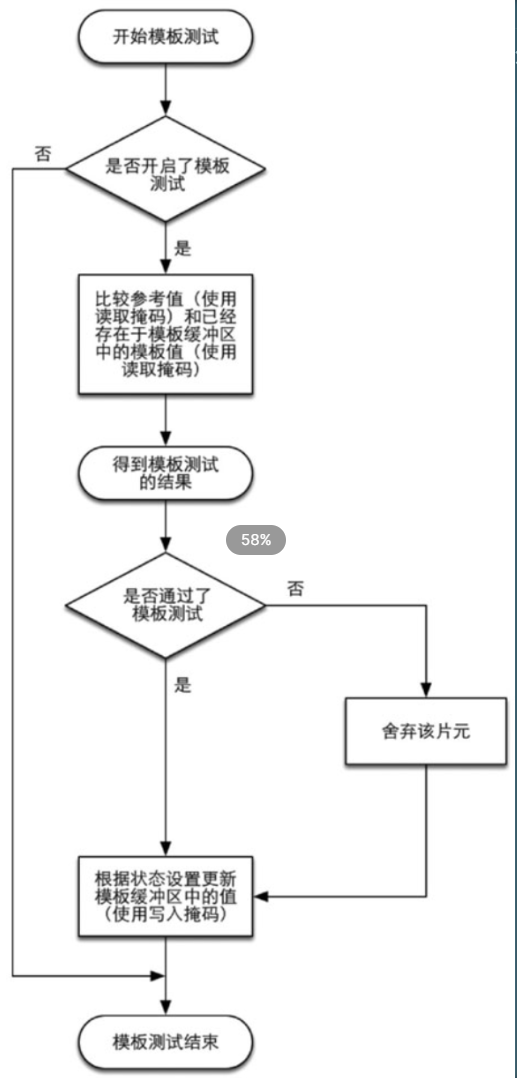
模板测试 - Stencil Test

  1. 模板测试需要模板缓存（Stencil Buffer），它与屏幕缓冲区的大小一致，每个片元在测试时都会先取得自己位置上的模板缓冲位置并与之比较，在通过测试后才被写入模板缓存中，在整个渲染帧结束前它是不会被重置的，也就是说，所有的模板测试共享一个模板缓存块。

image-20230205185519314

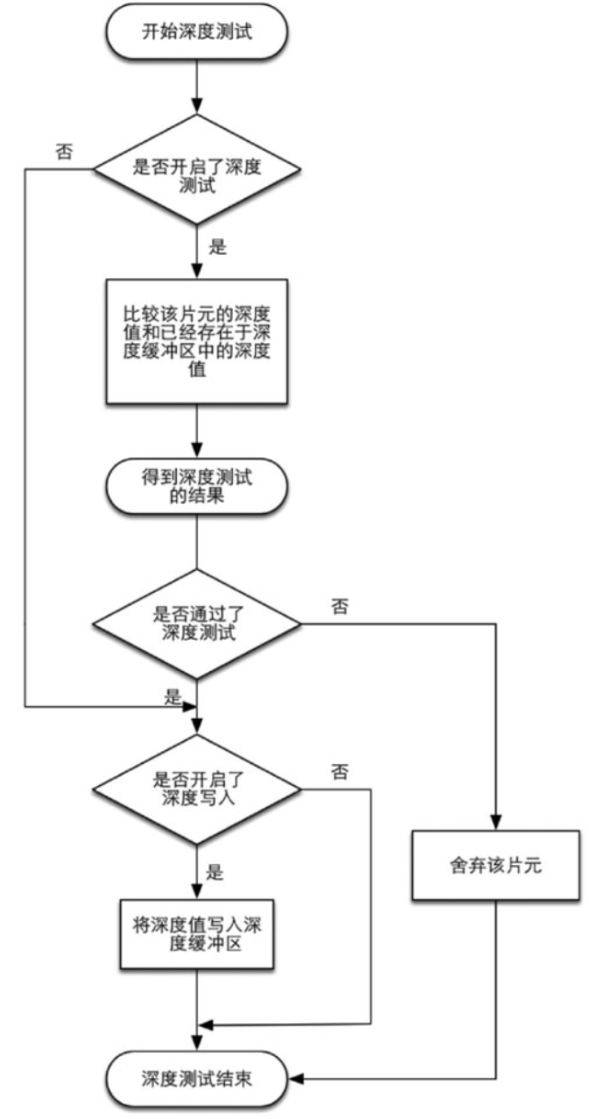
深度测试 - Depth Test

  1. 深度测试的作用是根据深度来判断和覆盖帧缓冲中的片元。片元中有深度信息，来源就是在归一化坐标后三角形顶点z轴上的值，三角形经过光栅化后，三角内片元的深度是三个顶点的z坐标的插值，深度测试依靠这个深度来判定是否需要覆盖已经写进帧缓冲里的片元.
  2. 在判定过程中，深度测试有自己的缓深度存，即（Z-Buffer），它可读可写，就是为片元深度信息判定而存在的。深度测试使用的是像素深度值。
  3. 深度测试工作分为两块，其中一块为是否开启深度测试，即 ZTest，另一块为是否把片元深度值写入深度缓存，即 ZWrite。所有片元只有在ZTest中与深度缓存中的深度值进行比较，并被判定通过，才能够通过ZWrite写入深度值。
  4. [[半透明物体]]应该关闭 ZWrite，打开 ZTest， 不然后面的片元会被抛弃，无法混合，因为不透明物体先渲染，所以不透明物体不会受到影响，但如果有多个半透明物体叠加渲染时，ZWrite 会导致后面的被抛弃，会让画面错乱。参考：[[渲染队列]]

image-20230205185541611

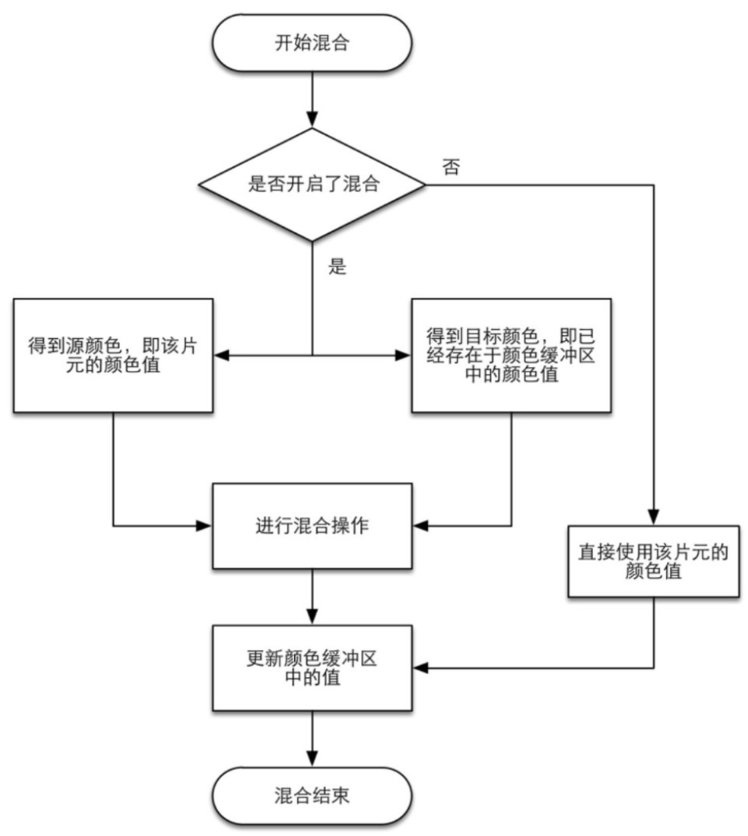
混合 - Blending

  1. 混合适用于半透明物体，只能在最后进行，因为之前的阶段，每个三角形，每个片元都是不认识的，没办法做混合。
  2. 混合过程：把当前片元的颜色值和帧缓存中的颜色值通过Apha值做计算。
  3. 混合方程：SrcColor×SrcFactor + DstColor × DstFactor

image-20230205185556331

显示画面

  1. 颜色缓冲区（Color Buffer）
  2. 双重缓冲（Double Buffering）
  3. 对场景的渲染写入后置缓冲（Back Buffer）
  4. 当前显示在屏幕上的图像位于前置缓冲（Front Bufer）

其他

  1. 画家算法处理前后关系，剔除关系

    • 不能处理互相交叉的情况
    • 最大的缺点是，需要按照深度排序图元，非常非常慢。

  2. Z-buffer（depth-buffer） Algorithm

    • gl_FragCoord.z. [0,1]

    • 显示深度图

      1
2
3
4

        float z = gl_FragCoord.z * 2.0 - 1.0;    // [0,1] -> [-1,+1]
  float depth = (2.0 * near * far) / (far + near - z * (far - near));
  depth = depth / far;				// 非线性深度值 -> 线性深度值
  gl_FragColor = vec4(vec3(depth), 1.0);
This post is licensed under CC BY 4.0 by the author.
Contents