Home 散列表
Post
Cancel

散列表

By Yzngo
Posted 2018-12-25 8 min read

散列表

  1. 散列表建立了Key和存储地址之间的一种直接映射关系，使查找速度极快。
  2. 如果冲突发生很多次，最坏情况下的时间复杂度是 $O(N)$，其中 N 是键的数量。
  3. 如果有一个不错的实现方式会将冲突数量保持在最低水平，在此情况下，时间复杂度是 $O(1)$。
  4. 哈希表使用列表作为桶存储 Key，使用链表存储 Value。如果列表空间太小，容易发生冲突；如果列表空间太大，会出现很多空位置，造成内存的浪费。

散列函数

  1. 哈希表会针对每一个Key进行一次Hash运算，从而确定在桶(bucket)中的地址。
  2. Hash函数本质上是从Key范围到地址范围的映射，Key的范围要远远大于地址的范围。
  3. 好的散列函数应尽量减少冲突。最好能够让地址等概率，均匀的分布在整个地址空间。
  4. 散列函数应尽可能简单，能够很快计算任一关键字对应的散列地址。
  5. C# Dictionary 中实例对象和字符串通过内存地址计算 HashCode。
  6. 编写类时可以重写 Object.GetHashCode() 方法提供自己的 HashCode 计算方法。
  7. 实践中，采用何种散列函数取决于关键字集合的情况，目标是使产生冲突的可能性尽可能的低。
  8. 常用的Hash函数：
    • 除留余数法：hash_key = Key % M

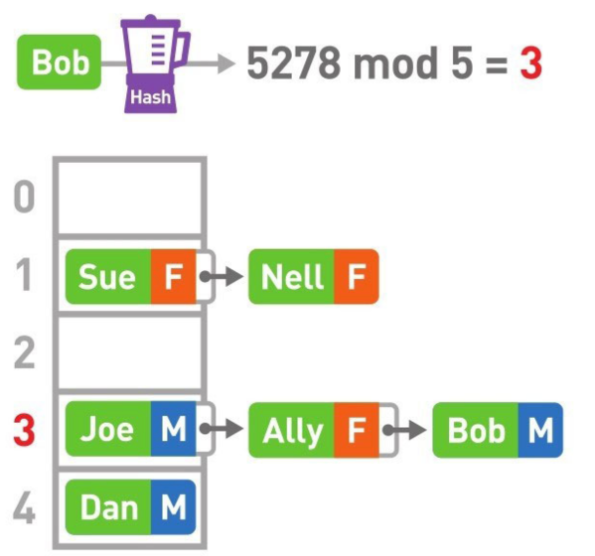
散列表中插入元素

  1. 使用散列函数计算出 Bob 的 Hash 值，再 mod 列表的长度，得到桶中的位置，插入。即： Hash(Key) % array_length
  2. 不同的 key 可能有相同地散列值，会被放到同一个桶中；不同的 key 算出不同的 Hash值 也有可能会被放到同一个桶中，因为列表长度始终有限。

image-20230205202151646

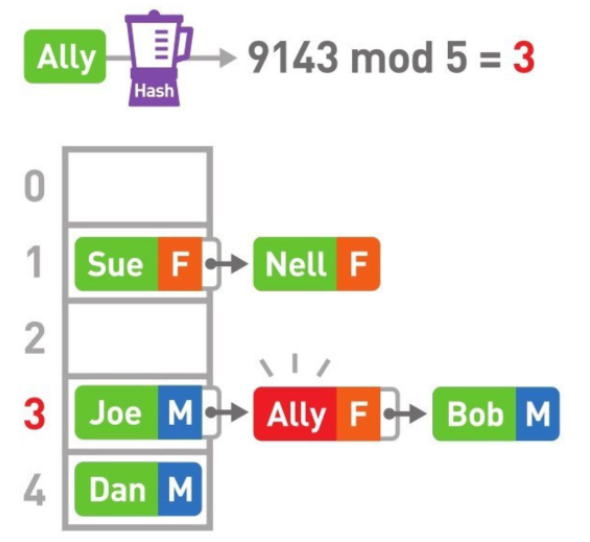
散列表中查找元素

  1. 使用散列函数计算出 Ally 的 Hash 值，再 mod 列表的长度，得到桶中的位置，再查找链表 ，看元素是否存在。

image-20230205202205462

除留余数法Hash函数

Hash 的意义在于把一个大的集合A（key的集合）映射到小的集合B（地址的集合）。

如果集合A的分布是均匀的，M取质数还是合数都可以，最后整个集合A都会被均匀的映射到B。

但是，很多情况下我们的元素分布是有非1步长的，比如集合 $A = \{ 0, 6, 12, 18, 24, 30, 36, … \}$ ，这时候就出现问题了。当M取合数时，比如 $M = 10$，我们来看看映射的情况。

0-> 0, 6->6, 12->2, 18->8, 24->4, 30->0, 36->6, …

此时很容易发现，最后映射到了集合 $B = \{0, 6, 2, 8, 4\} = \{0, 2, 4, 6, 8\}$，和理想中的 $\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$ 差距很大。

回到代数形式上来看，在Key与M最大公因数为1的情况下，Key % M 后可以得到的一系列的余数 r，而全体余数 r 的集合R就是 $\{0, 1, 2, …, M-1\}$。每个余数 r 代表了一个 N 的集合，比如在上面的例子中余数0代表了N的集合 ${0, 10, 20, 30, …}$，这个集合就叫做“同余类”。即余数集合R中有M个余数，每个余数 r 代表一个同余类。现在思路就很清晰了，我们最理想的方式就是将集合A映射到余数集合R上，即B = R。

接下来我们讨论一下为什么有时候无法完全利用余数集合R：

假设 N = kn, M = km， N 和 M 存在最大公因数 k，此时可以将 N % M = r 转化为公式 N = Mq + r ，即 kn = kmq + r。其中 q 是商，r 是余数。表面上 r 的取值范围是 $\{0, 1, 2, …, M-1\}$（忽视了只有N与M最大公因数为1时，才能取整个余数集合R的定理），一片和谐。但是可以对公式进行稍微的变换，n = mq + (r/k)，由于 n 和 mq 都是整数，则 (r/k) 也是整数。此时我们看到 (r/k) 的取值范围是 $\{0, 1, 2, …, m\} = \{0, 1, 2, …, M/k\}$ 。恢复到原式，也是就r的“实际”取值范围是 {0, k, 2*k, 3*k, …, m*k} ，缩小了k倍。

一切都明了了，我们最后的目标就是保证Key与M最大公因数为1。最简单的方式就是直接取M为质数！

一句话总结：Key和M的最大公因数越少，冲突的可能性越低，对余数集合R的利用率越高。

处理冲突的方法

  1. 处理 Hash 冲突的方法有：开放定址法，再Hash法，拉链法，建立公共溢出区等。

  2. C# Dictionary 字典类使用拉链法解决冲突。

  3. 查找过程：
    • 给定Key，根据Hash函数求得Hash地址。
    • 如果桶中此索引处没有记录，表示查找不成功。
    • 否则依次比较链表中的关键字，若找到与给定值相等的，则查找成功，否则失败。

image-20230205202219357

质数集合

1
2
3
4
5
6
7
8
9
10
11

public static readonly int[] primes = {
        3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 131, 163, 197, 239, 
            293, 353, 431, 521, 631, 761, 919,
        1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 
            8419, 10103, 12143, 14591,
        17519, 21023, 25229, 30293, 36353, 43627, 52361, 62851, 75431, 90523, 
            108631, 130363, 156437,
        187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 
            807403, 968897, 1162687, 1395263,
        1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 
            7199369};
This post is licensed under CC BY 4.0 by the author.
Contents