算法特点
- 序列很短的话,比如少于16个元素,就不要用快速排序了,换插入排序。
- 快速排序基于分治和递归。
- 目标是把所有比基准元素小的元素移到基准元素的左边,把比基准元素大的移到右边。
算法步骤
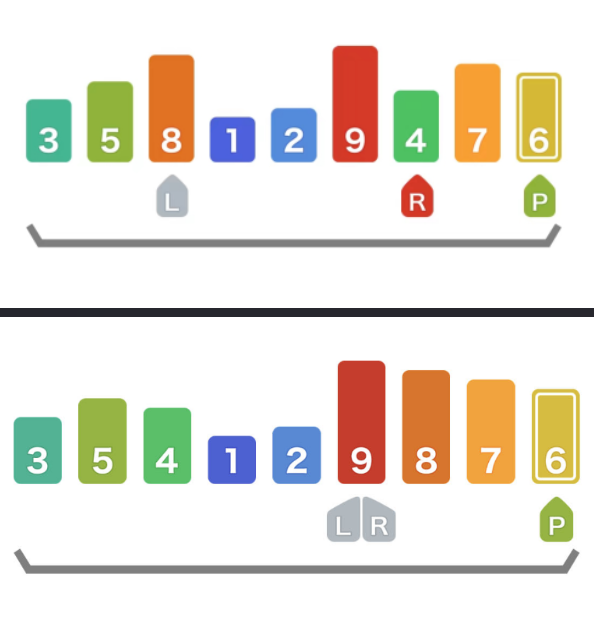
- 先从序列中随机选择一个元素作为基准元素 Pivot,选哪个都没有影响,可以选末尾的。
- 从左往右找一个比 pivot 大的元素 L,再从右往左找一个比 pivot 小的元素 R,交换 L 和 R,重复此过程,直到左右游标相遇在 LR,把 LR 和 Pivot 交换,此时 Pivot 归位。pivot 把序列分成了左右两部分。
- 分别在左右两部分上重复步骤1,直到划分后的序列中只剩下一个元素。
复杂度
时间复杂度
- 平均/最优时间复杂度 $O(nlogn)$,其中logn为调用栈的深度
- 想象10000个元素的均匀序列,每一趟排序后,待排序序列平均分为两组,这样只需要 2logn 趟就能排好,所以T=O(nlogn)
- 如果序列原本即有序,最坏时间复杂度为 $O(n^2)$
- 想象10000个元素的有序序列,每一趟排序后,待排序序列只会少1个元素,这样一共需要n趟才能排好。所以T = $O(n^n)$
空间复杂度
- 快排没有开辟空间,但是使用了递归,递归会开辟栈帧,所以空间复杂度就是调用栈的深度,即 S = O(logn)。
- 如果序列原本就是有序排列,此时最坏空间复杂度 S = O(n)。
稳定性
- 不稳定