平面三角形的剖分问题

概念

1. 三角形作为最简单的平面图形，较其他平面图形在计算机表示，分析和处理等方便要方便的多。
2. 平面三角形的剖分问题意思是在一张平面图上有很多颜色，颜色边界形成了很多点和线，根据这些点和线将这幅图分解成由许多三角形组成的多边形。
3. 三角剖分是研究其他很多问题的前提。

应用领域

1. 模式识别
2. 图像处理
3. 计算机图形学
4. 机器人领域

Delaunay三角剖分算法

1. Delaunay三角剖分算法是一个准则，满足此准则的算法即同时满足全局和局部最优。
2. Delaunay三角剖分的三角形必须满足以下三个要求：
   • 除了端点，三角形的边不包含其他任何点。
   • 除了在点上的连接，没有任何一条边是相交的。
   • 所有的面都是三角形，且所有三角形的合集是所有点集合的凸包。

Bowyer-Watson算法

切耳(Ear Clipping)算法

1. 切耳算法需要工作在 [[简单多边形]] 上。
2. 耳点：指多边形中相邻的三个顶点V0、V1、V2形成的三角形里，不包含任何其他顶点，并且如果V1点是凸点，即V0-V1的连线与V1-V2的连线之间形成的夹角小于180度，则认为V1是耳点。所以，一个由4个顶点组成的多边形中，至少有2个耳点。
3. 耳朵三角形：三角形顶点中有耳点的就叫耳朵三角形。
4. 切耳算法的步骤：
   • 第一，找到一个耳点。
   • 第二，记录这个耳朵三角形，然后去掉这个耳朵点，基于剩余的顶点继续回到第一步。
   • 第三，直到剩下的最后3个点形成一个三角形并记录下来，把所有记录的三角形拼接起来就形成了三角化网格。
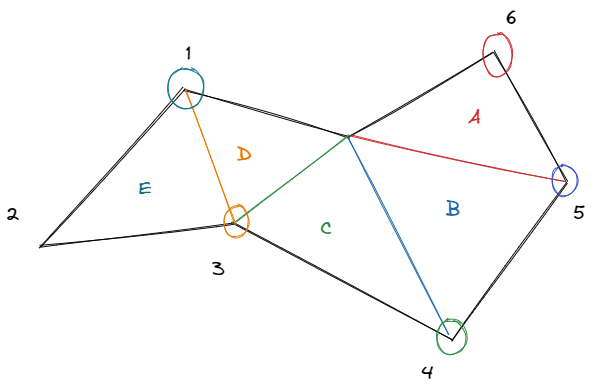
5. 按照切耳算法的规则，以下图可以按照65431的顺序选点，按照 ABCDE的顺序切分。