堆排序

优先队列

1. 优先队列可以自由添加数据，但取出数据时要从最小值开始按顺序取出。
2. 堆是最高效的优先队列（Priority Queue）

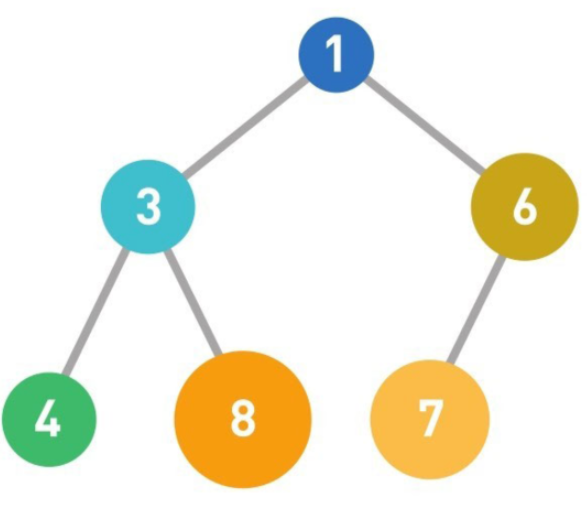
小根堆

1. 小根堆的子结点必定大于父结点，最小值存储在根结点中。
2. 堆是一种完全[[二叉树]]结构，可以用一维数组表示，这样会让效率更高，因为内存是连续的。
3. 堆构建完成后能够得到一个头顶着最大值或最小值的数据结构，这种数据结构更有利于获取根节点的最大最小值节点。在后面的程序逻辑中，当需要插入新元素、修改旧元素及推出最大最小值时，效率都比较高。

添加数据

1. 插入的元素先放在二叉树的最后一个叶子节点的位置上。
2. 如果父结点大于子结点，交换父子结点的位置。 重复此操作，直到不再需要交换为止。

取出数据

1. 删除根节点。
2. （重构堆1）把最后一个叶子节点拿过来放到根上。
3. （重构堆2）如果父结点大于子结点，把父结点同子结点中较小的那个交换。 重复此操作，直到不再需要交换为止。

时间复杂度

1. 取出最小值：O(1)
2. 每轮构造或重构堆：$O(logn)$ - 即树的高度
3. 堆排序的时间复杂度：$O(nlogn)$

堆的应用

1. 堆是最高效的优先队列。[[Dijkstra最短路径算法]]，每一步都需要从候补顶点中选择距离起点最近的那个顶点，在顶点的选择上可以用到堆。
2. 堆排序也常用于 [[A*寻路算法]]。获取最大最小值时十分高效的特点，导致它在寻路系统的A星算法中特别有用。