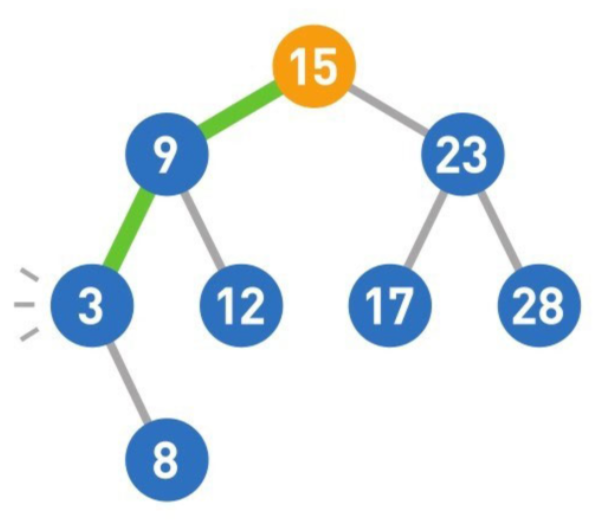
二叉查找树

二叉查找树

1. 二叉查找树左边的子节点一定比父节点小，右边的子节点一定比父节点大。

二叉查找树的性质

1. 最小结点在左下的末端。如上图中的 3。
2. 最大结点在右下的末端。如上图中的 28。

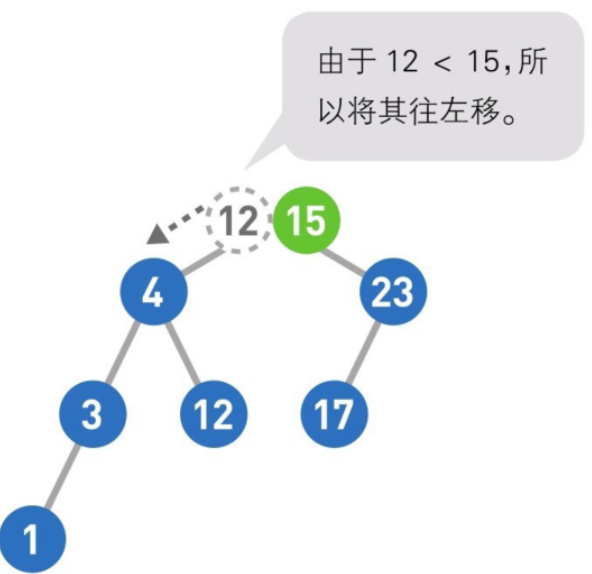
添加数据

1. 从根结点开始寻找插入位置，将想要添加的数据和结点比较。如果更小，就往左移；如果更大，就往右移。直到前面没有结点了，就把添加的数据作为叶子结点添加到二叉查找树中。

删除数据

1. 如果删除的结点没有子结点，直接删除即可。
2. 如果删除的结点只有一个子结点，就先删除目标结点，然后把子结点移动到被删除结点的位置上。
3. 如果删除的结点有两个子结点，就先删除目标结点，然后在被删除结点的左子树中寻找最大的结点，把它移动到被删除结点的位置上。如果移动的结点还有子结点，就递归的执行此过程。

查找结点

1. 从根结点开始查找，小于结点往左移动，大于结点往右移动。

时间复杂度

1. 查找：$O (logn)$
2. 添加：$O (logn)$
3. 删除：$O (logn)$

和二分查找比较

1. 二叉查找树是二分查找算法思想的树形结构体现。
2. 算法的方式与二分查找算法类似，不同之处在于二分查找树构建出来的树形结构，由于原始数据的排列不同，有可能导致深度很大的二叉树犹如直线连接的节点，因此它是一个不稳定的查找方式，搜索的速度由原始数据的排列方式决定，若排列的顺序不好，则速度就不快，因此二叉树的稳定性并不高。